The relationship of cumulative incidence to incidence rate
This is a concept I've struggled with for several years. I was trained that the "[incidence] rate will always be larger than the cumulative incidence" (Szklo and Nieto, Epidemiology, pg 69). But why? Yes, there are mathematical relationships between the two (see pg 70, Exhibit 2-2) or this discussion, which references Rothman. But I need a concrete, intuitive way to think of this. Well, I think I came up with one.
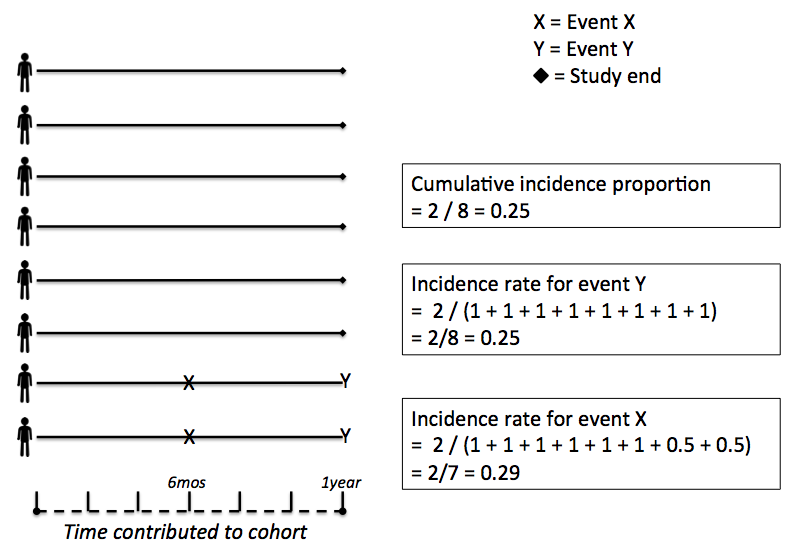
This is a super contrived cohort. We have eight individuals who have completed follow up after one year with no censoring. If we assume that the event of interest occurs at the conclusion of the study (event Y), the absolute value (ignoring units) of the cumulative incidence proportion will equal the incidence rate, as the denominators are both equal. However, if the event of interest occurs at any time before the conclusion of the study (event X), the incorporation of time-to-event will shrink the denominator, thereby increasing the calculated value of the rate. The incorporation of censoring will further shrink the denominator. This comparison is possible because cumulative incidence and person-time are based on the same time unit of one year and per person-year, respectively.
When there is complete follow up, the relationship between cumulative incidence and incidence rate is apparent. But how does censoring affect this? Altering the above example to include a few right censored (i.e., loss to follow-up) individuals and more interesting time-to-event cases, yields:
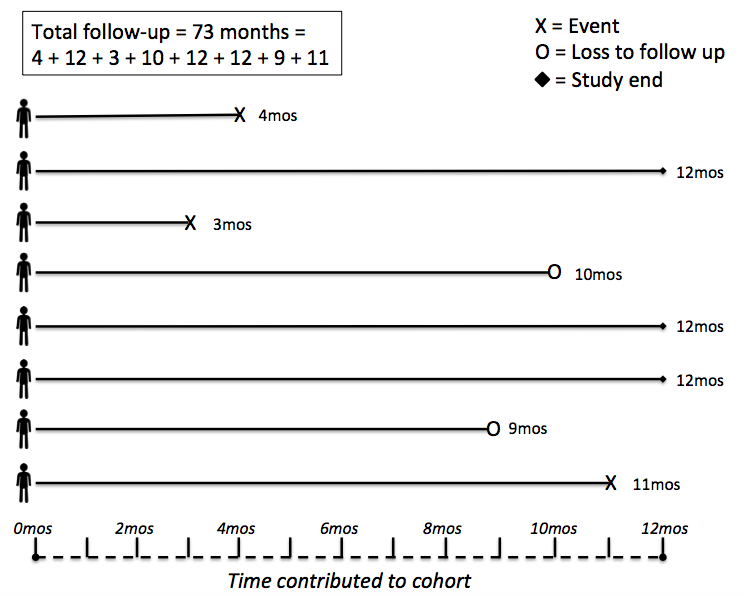
Without taking into account censoring, the cumulative incidence = 3 / 8 = 0.375, and the incidence rate = 3 / (73 / 12) = 0.493. Note that dividing the denominator by 12 converted months to a year, necessary to compare the incidence calculations. As expected, the incidence rate was larger. The numerators remained the same and the denominator shrunk in the incidence rate measure due to accounting for time-to-event and loss to follow-up.
With the knowledge of follow-up time, the incidence rate is the preferred measure. But suppose that follow-up time is unknown. Can we do better a better job of approximating the incidence rate from cumulative incidence? As it happens, yes, using a conditional probabilities approach (similar to Kaplan-Meier) that estimates cumulative incidence (cumulative probability) of event when there is independence of censoring and survival, calculated = (3 + (3/6) + (3/6)) / 8 = 0.500. The numerator is formed by adding the total number of events at one year, plus the conditional probability that each censored individual experienced the outcome at one year, based upon the non-censored individuals. Now the value of the cumulative incidence is much closer to the incidence rate. Essentially this calculation posits a probability that an individual who left the study early developed the outcome, and this probability is based on the probabilities of those we know about at the conclusion of the study. Voila!
Cite: Goldstein ND. The relationship of cumulative incidence to incidence rate. Oct 27, 2015. DOI: 10.17918/goldsteinepi.