Towards improving the concepts of internal and external validity using a computer science metaphor
May 25, 2021: Updated
Introduction
The concepts of internal validity and external validity have been well discussed in epidemiology (Hernan and Robbins, 2020). There are theoretical (e.g., directed acyclic graphs) and mathematical representations of these two constructs, which, when ignored, may negate the value of a particular study. Educators are frequently reminded of the difficulty that students have in appreciating internal and external validity, such as the relationship between selection bias and representativeness or confusion between generalizability and transportability. Recently, the concept of target validity has been proposed as a way of unifying this view, eschewing the need for a distinction between internal and external validity and focusing on a single measure known as target bias (Westreich et al., 2019). When target bias is zero, the study can be said to be valid. As many epidemiologists have been trained in an era prior to this proposal and traditional epidemiology textbooks continue to refer to internal and external validity separately (Szklo and Nieto, 2018; Rothman et al., 2008), there will be a continuing struggle to appreciate these concepts. What follows is an attempt to clarify these concepts through simple, visual schematics using a metaphor of inputs and outputs borrowed from computer science. The basis of these visual aids is conceptualizing internal validity as inputs to the analysis and external validity as outputs from the analysis. In other words, decisions and assumptions made about the participants or their health measures (the inputs) impacts the analysis, whereas the evidence garnered from the analysis (the outputs) impacts the inference made to various populations. Fundamental to this presentation is the study is etiologic in nature, seeking to measure a health outcome related to some putative exposure.
Inputs and Outputs
Figure 1 depicts a study that is free from bias; the inputs and outputs were both valid. When drawing the study sample or population (i.e., the participants of the study), there were no systematic errors in selecting participants or measuring variables, and all relevant variables were included. Sampling error was minimized, and the study was analyzed correctly. The results are applicable to the broader population that the study sample was drawn from as well as other, different populations. In other words, the participants were exchangeable with other groups.
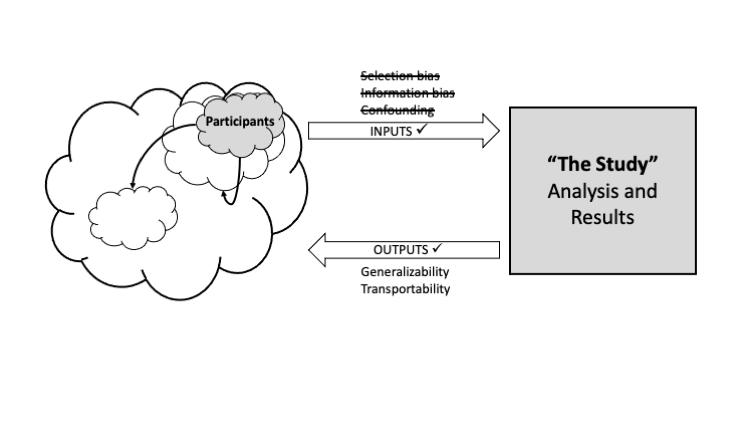 Figure 1. A study where the inputs and outputs are valid: internal and external validity.
Figure 1. A study where the inputs and outputs are valid: internal and external validity.
Figure 2 depicts a study where there was a systematic error that resulted in a lack of internal validity, thus one or more of the inputs was flawed. The study population may have been preferentially selected on the basis of the exposure and outcome (selection bias), may have mismeasured an important variable (information bias), or may have failed to adequately consider an influential extraneous variable (confounding). Internally validity has also been described as problem of missing data (Howe et al., 2015), in that data may be missing on the non-participants (selection bias), the true value of measurements (information bias), or the measurement of influential variables (confounding). In any or all of these cases, these "missing data" impacted the results obtained during analysis. It is also important to recognize that decisions on the treatment of missing data may result in a manifestation of any of these concepts; for example, a complete case analysis that has excluded participants differentially on the exposure and outcome can induce a selection bias. Despite the potential for external validity, in that the participants may have been representative of a community targeted for inference (except in the case of a selection bias), without internal validity we should be cautious in making any such inference. Internal validity is a prerequisite to external validity, and to quote another computer science adage, "garbage in, garbage out."
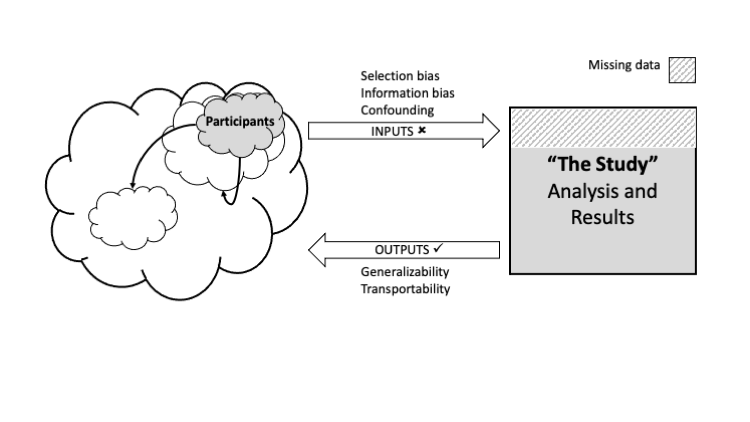 Figure 2. A study where the inputs are invalid but the outputs are valid: external validity without internal validity.
Figure 2. A study where the inputs are invalid but the outputs are valid: external validity without internal validity.
Figure 3 depicts a study that is internally valid yet lacks external validity and thus one or more of the outputs are problematic. The participants may be nonrepresentative of some target population: they lack exchangeability. For example, suppose study participants were randomly drawn from a hospital that is highly regarded for the treatment of cancer and the desired inference was the local community. The participants in the study are likely not representative of the hospital's catchment area, yet the study was free from any selection bias because we did not preferentially select patient's contingent on an exposure and outcome, and the sample was randomly obtained. In this case, the study lacks generalizability to the local community but may be transportable to other settings with similar characteristics to the patients who have traveled to this hospital. In another example, suppose the study participants were again randomly drawn from a hospital, but this time at an urban safety net hospital that serves groups that have been historically marginalized. Again, we did not preferentially select patient's contingent on an exposure and outcome, so the results are not subject to selection bias, but in this case the participants were representative over their local community (the one served by this safety net hospital). In this case the results may not transport from the marginalized group seen at the local hospital to a more affluent group seen at a different hospital in a different community. In other words, there is a lack of transportability to another, more affluent community, but the study maintains generalizability to the local community. A key feature to both threats to external validity show in Figure 3 and presented in these two examples is the presence of an effect modifier. Some feature of the target population to which we wish to apply our inference is modifying the exposure to outcome relation. Continuing with the examples, this could be socioeconomic position as a surrogate for access to healthcare. As with the case of flawed inputs, problematic outputs are a warning for the epidemiologist to reconsider any exposure to outcome effect outside of the confines of the study participants.
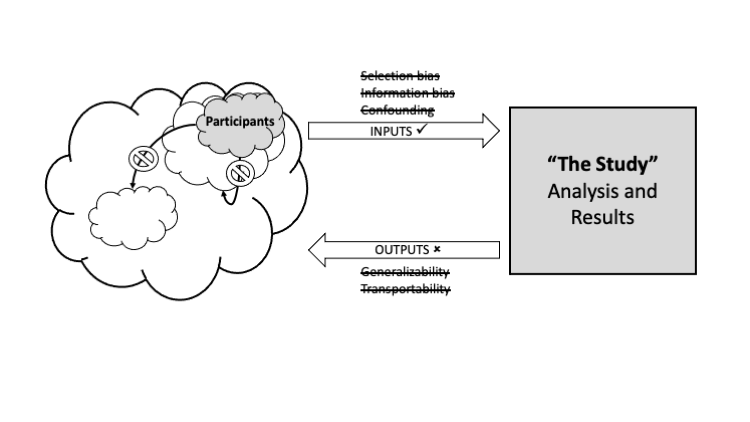 Figure 3. A study where the inputs are valid but the outputs are invalid; internal validity without external validity.
Figure 3. A study where the inputs are valid but the outputs are invalid; internal validity without external validity.
Discussion
Under this computer science metaphor, inputs capture the processes antecedent to analysis, while outputs represent the application of the results to various places and populations. This builds upon the concepts of internal and external validity by identifying a directionality to the mechanisms and providing a logical connection between the steps typically undertaken in an epidemiological study. Although inputs and outputs are depicted separately in the figures, they are by no means mutually exclusive. One can have problems with both the inputs and outputs concurrently (a combination of Figure 2 & 3), nor is it possible to identify a hierarchy to them (inputs are not greater than outputs, and outputs are not greater than inputs) (Westreich et al., 2019). Additionally, the notion of a study free from all biases may be an impossibility as there may always be a conceivable reason why an input or output is not perfect. Rather than striving for perfection, epidemiologists focus on understanding the presence and impact of threats to validity, and if necessary, perform a quantitative bias analysis.
The notion of representativeness warrants further comment as it may impact both inputs and outputs. In a strict sense, any deviation from randomness when selecting the study participants from a target population may result in a non-representative sample and potentially impact results. If this deviation is patterned on the exposure and outcome then this can be termed a selection bias (invalid inputs) (Richiardi et al., 2013). The term "selection bias" in this case is specific to the epidemiological definition; other fields use the same term but most likely are referring to the notion of sampling error. If the study sample is a true random sample from the target population, then we have avoided both sampling error and selection bias, and achieved representativeness. If the study sample is not a random sample from the target population, which is most likely the case in most epidemiology studies, and also not conditional on exposure and outcome, then sampling error and representativeness are brought to mind as opposed to selection bias. This could impact the estimates of prevalence of various attributes in the sample, but would not alter the correlation between the exposure and outcome. On the other hand, some have argued that true representativeness is undesirable in scientific study in that the inference may be limited to only the participants in the study, and thus lack any external validity (invalid outputs) (Rothman et al., 2013). This is criticism lobbed at clinical trials, where strict inclusion and exclusion criteria are present (Greenhouse et al., 2008). An overly representative sample may result in invalid outputs while an underly representative sample may result in invalid inputs.
A limitation and necessary consequence of these visual depictions is the simplification of nuanced concepts into boxes and arrows. It is not the intention of this metaphor to redefine or consider all possible types of biases, such as would be found in the Dictionary of Epidemiology (Porta, 2014). Rather, the intention was to provide an aid that is useful for recognizing the meaning and relationship between these threats to validity as opposed to guidance or statistical tools for remediating them. Further, some of the validity distinctions made herein are semantic, and use of the term "bias" can be rather liberal, as it has broad meaning in epidemiology and beyond. For example, the typical internal validity threats - bias and confounding - begin to break down in the face of descriptive studies that consider only a single measure, such as a prevalence study without the search for risk factors. That is, from a strict sense, one cannot have selection bias, differential misclassification, or confounding without at least two variables under consideration, which in its purest form would be the exposure and the outcome. As long as one is capable of identifying potential for bias, the exact distinction becomes less critical. For those who would like such distinction, the computer science metaphor provides an intuitive structuring.
References
- Hernan MA, Robins JM (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC
- Westreich D, Edwards JK, Lesko CR, Cole SR, Stuart EA. Target Validity and the Hierarchy of Study Designs. Am J Epidemiol. 2019 Feb 1;188(2):438-443.
- Szklo M, Nieto J (2018). Epidemiology: Beyond the Basics. Burlington: Jones & Bartlett Learning.
- Rothman KJ, Greenland S, Lash TL (2008). Modern Epidemiology. Philadelphia: Lippincott Williams & Wilkins.
- Howe CJ, Cain LE, Hogan JW. Are all biases missing data problems? Curr Epidemiol Rep. 2015 Sep 1;2(3):162-171.
- Richiardi L, Pizzi C, Pearce N. Commentary: Representativeness is usually not necessary and often should be avoided. Int J Epidemiol. 2013 Aug;42(4):1018-22.
- Rothman KJ, Gallacher JE, Hatch EE. Why representativeness should be avoided. Int J Epidemiol. 2013 Aug;42(4):1012-4.
- Greenhouse JB, Kaizar EE, Kelleher K, et al. Generalizing from clinical trial data: a case study. The risk of suicidality among pediatric antidepressant users. Stat Med. 2008;27(11):1801-1813.
- Porta M (2014). A Dictionary of Epidemiology. New York: Oxford University Press.
Cite: Goldstein ND. Towards improving the concepts of internal and external validity using a computer science metaphor. Feb 26, 2021. DOI: 10.17918/goldsteinepi.