Social Network Analysis in Epidemiology: Part 1
I recently attended training in social network analysis geared towards infectious disease epidemiology, and am beginning a three-part series of blog posts as a way of remembering what I learned. Network analysis is not new; it has been used in the social sciences for years. Essentially a network defines a group of people and their interactions with each other. It is an individual level modeling approach. By modeling this we can assess who interacts with whom, are there patterns, and what are the ramifications. Historically the statistical modeling necessary for this type of analysis was complex, and understood by only a handful of researchers out there. However, the science has progressed rapidly and is now quite approachable with pre-written network analysis functions in R (and probably other statistical software as well).
One of the better-written introductions to social network analysis is the "Birds of a Feather…" paper by Goodreau, et al. Goodreau used data from the National Longitudinal Survey of Adolescent Health (Add Health) and modeling friendship formation and social networks at several schools. They sought to understand how sociodemographic structure influences friendships.
This is all well and good, but how does that help the infectious disease epidemiologist? Let's take a brief tangent (Part 1) and then we'll arc back into network analysis (Parts 2 & 3). Suppose we are interested in studying the incidence and prevalence of an epidemic, HIV being the classic example. Traditional epidemiology teaches a compartmental approach to modeling disease epidemics: the SI, SIS, SIR, SIRS, and etc. models. For those who have been out of the infectious disease world for a while, "S" means the susceptible (to a disease) population, "I" means the infected, "R" is recovered and immune.
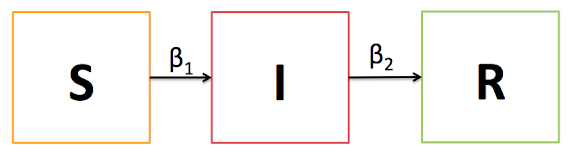
The basic idea is that people flow from one state (compartment) to another at some fixed rate, usually denoted by the greek letter beta, where beta1 is the infection rate and beta2 is the recovery rate. We use these models to track the progress of an epidemic over time and can estimate incidence and prevalence.
This model is very simplistic and makes a lot of assumptions. First, everyone is vulnerable in the population. Second, the infection rate is constant. Third, the recovery rate is constant. Fourth, once recovered you are immune for life. Fifth, the population is closed. I could go on and on. Recognizing this, there have been many additions to the basic model, such as allowing births, deaths, and differential compartmental flow rates depending on characteristics of the population. Suppose we wish to complicate this model just a little bit by saying that age and sex are important characteristics. To keep this manageable, we'll dichotomize age into young and old groups, and acknowledge only two biologic sexes: male and female. Let's also just work on the infection rate problem (we'll say that there is no recovery, such as for HIV infection). If we assume that each characteristic has its own infection rate, all of the sudden we have four betas and eight compartments to keep track of (as opposed to one beta and two compartments).
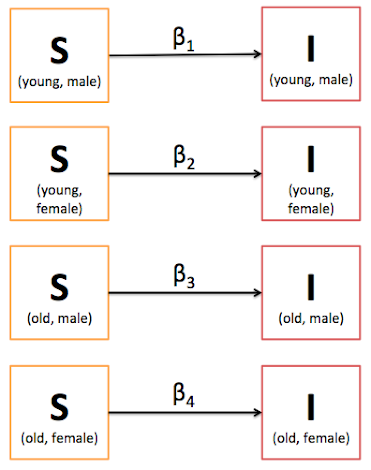
The number of rates and compartments will grow exponentially based on the number of characteristics of the population that are important to track. The methods to solve the differential equations quickly become unwieldy in the presence of a large number of betas. This is why many compartmental modeling papers that you'll encounter in literature only consider a few characteristics at a time. Further, the simple versions of these models only consider "who you are" not "who you interact with". As these compartmental models consider groups of people (they are not individual level) the notion of individuals interacting is unattainable. What was needed was a way to combine the network modeling approach of "who you interact with" while keeping track of the disease state of the individual. Enter EpiModel. Yet before exploring the capabilities of EpiModel in Part 3, Part 2 will review terminology and concepts of analyzing social networks and basic graph theory.
...continue to Part 2...
Cite: Goldstein ND. Social Network Analysis in Epidemiology: Part 1. Jul 6, 2016. DOI: 10.17918/goldsteinepi.